Всем ОЧЕВИДНО?
Или у нас как в сказке про голого короля?
Одна мудрость на всех: "Молчи дурак- умнее будешь"
А ведь не будешь!
Давайте я изложу. Хочется с новой игрушкой проиграться.
Начнем с начала (каламбур-с!). То есть с закона всемирного тяготения:

Это сила F. Работа же, это противодействие силе F на пути s. А=Fs
Это если сила постоянная. А если она сама функция от пути, то мы имеем интеграл. Наш случай тем "сложней" что интеграл несобственный. Нижний предел - начальное расстояние r, с которог мы удаляем объект на бесконечность, а верхний - бесконечность. Но на самом деле это ерунда. Решаем.
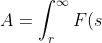ds=\int_{r}^{\infty}G\frac{Mm}{s^{2}}ds=)
=G\frac{Mm}{r})
То есть это работа (необходимая энергия) для удаления на бесконечность от тела массой M массы m, центры масс которых изначально находится на расстоянии r. Например так надо считать запуск космического корабля в бесконечность.
Теперь что делать с Землей? Мы упрощенно ее считаем сферой РАВНОМЕРНОЙ плотности радиусом R и массой M.
И нам поступила замечательная подсказка от нашего уважаемого "трилобита" снимать с нашей сферы снимать тоненькие шкурки массой m
i и удалять их в бесконечность. Снимать и удалять. Снимать и удалять. Диаметр планеты постепенно уменьшится от R до 0. Вот она и кончилась!
Дело сделано!
То есть работа по распылению нашей планеты это сумма работ по удалению на бесконечность каждого слоя:

(1)
Здесь с каждым шагом все меняется. mi (масса снимаемой кожуры) становится меньше (площадь поверхности остаточной сферы ведь уменьшается). M
i тоже становится меньше (объем гравитационной массы ядра, тает. Тает и масса). То есть гравитационная яма становится все мельче, мельче, мельче. Ну и сам диаметр r
i тоже становится меньше, меньше, меньше... Всякий раз на толщину слоя
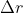
.
Вот и давайте все это считать.
Прежде всего нам понадобится знать плотность материала из которого состоит Земля
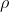
. Это масса Земли деленная на объем Земли (который мы находим как объем сферы радиусом R):

Теперь мы можем обе массы выразить через M и R.
Прежде всего m
i. Она равно опять же объему умноженному на плотность (вот зачем нужна плотность). Объем снимаемой кожуры - это площадь сферы радиусом r
i умноженная на ее толщину
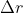
. В итоге:

(2)
Не запутайтесь,
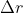
в произведении я вынес назад.
Что с массой "ядра"?
Не хватайтесь за плотность опять.
Здесь нам плотность не понадобится. Все проще. Масса ядра M
i будет во столько же раз меньше массы Земли M, во сколько меньше соотношение их объемов. Значит соотношение объемов равно соотношению кубов их радиусов. Поэтому масса ядра:

(3)
Физическая часть задачи фактически решена. Поставляем в (1) выражения (2) и (3):

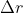
я опять отодвинул назад. Можно было бы сказать что

, а
 (поправил)
(поправил)И в принципе можно считать все численно... С некоторой точность. Благо у всех на столе машина о которой Исаак Ньютон и помыслить, наверное, не мог...
Но нам это все не надо. Мы заявляем что
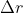
стремится на 0 и обзовем его dr, r
i становится интегрируемой переменной r, а сигму заменим на определенный интеграл (вообще надо было ввести предел... но уже не буду):

Это и есть предложенная мне подсказка. Осталось все это чисто механически решить. Приводим подобные, выносим константы за знак интеграла. Получаем примитивную функцию (не так страшен черт...) и легко находим первообразную (вот откуда появляется 5-ка в "3/5" откуда 3-йка можно догадаться сразу). Потом собственно получаем сам определенный интеграл.

=\frac{3}{5}\frac{GM^2}{R})
Вот собственно и сказочке конец, а кто слушал...
Вот вам "очевидность" olenellus, переведенная в очевидность Семенова...

И еще. Никто никогда вам не будет разжевывать подобные вещи вот так как я сейчас. Я разжевывал потому что я сам дурак. Да и то, мне сегодня очень хотелось проиграться с новым инструментом. Потренироваться.
Вот я и совместил.
Но настоящие спецы лаконичны до омерзения.
И дело даже не в том что маститые уже тренированные и им лень разжевывать. Дело не в их зазнайстве, кулуарности, нежелании вам помочь.
Дело в том что маститые спецы, как правило и педагоги. Научился сам - научи другого. Таков закон ИХ жизни. А они сами тоже когда-то учились. И они прекрасно знают что от такого вот разжевывания нет никакой пользы тому кто ДЕЙСТВИТЕЛЬНО пытается чему-то научиться и понят. Да, на лекциях студент списывает и ему все вроде ясно. Но когда он беретесь за ручку сами что-то...

Единственная причина почему я плохо шарю - я мало сидел сам. Пару интегралов, пару дифур (и половину занятий я пропустил в субботу потому что летел на междугородном к жене).
Есть вещи, которые надо делать самому. Искать самому. Самому мучаться. И учиться не бояться этого. Учиться не сдаваться. Учиться искать. И учиться получать (предвкушать) удовольствие. Нет царской дороги в математику, как известно.
Поэтому когда зубры вам объясняют они вам подсказывают ПО МИНИМУМУ. Очень скупо. Нащупывая ваш уровень знаний. И не спешат вам испортить удовольствие собственного поиска вкусных деталей самому...
Сначала двойной интеграл. "Очевидно"... Не справился? Вот еще подсказка. "Ну совсем же очевидно!!!" И ждут когда пойдет у вас само.
Для людей случайных со стороны это может выглядеть как зазнайство.
Но это только так кажется.
От добра ведь добра не ищут...
Кстати в б-СССР эта метода ТРАДИЦИОННО была куда жестче чем "за бугром". Возможно даже порой чересчур жесткая. Но результаты, как мы знаем, она дала удивительно хорошие.