dti≠dti
Время полёта i-го снаряда много больше промежутка времени между ударами i-го и i-1 снарядов о магнитное зерцало....
Или я ошибаюсь?
dt - это дельта-тэ. Что бы не ставить значок дельта (трехугольник) я использую букву d. Это конечно сбивает (мол, дифференциал). Но у нас тут простая школьная геометрия повсюду. Тут нет на самом деле кривых. Тут ломаные (и это больше похоже на правду, хотя мат физики сказали бы что все же подобную модель лучше апроксимировать непрерывной моделью).
Теперь о времени полёта. Они вообще никак не связаны. Могут быть больше, могут меньше.
Нам нужно решение общего случая и вот оно (предыдущее, неверное было частное, сейчас мы его тоже увидим).
Рассмотрим случай, когда время полета заметно больше интервала между столкновениями.

Смотрите. Ломаная зелёного цвета - это траектория зонда. Красные - снаряды. После каждого столкновение зонд движется чуть быстрей (наклон его траектории меняется). Я выделил ярко синим неизвестные на i-том шаге модели.
абсолютные моменты времени обозначаются t. Если при t штрих - это момент столкновения снаряда с зондом. Если без штриха - это момент выстрела снаряда. Снарядов много, поэтому их еще и нумеруют индексом внизу. Так как нам нужна универсальная формула, которая опирается на данные из предыдущих расчетов то мы нумеруем снаряды из произвольного места назад: i, i-1, i-2, ... и т.д.
S - это дистанция в пространстве от точки запуска снарядов к зонду. L - интервал в пространстве.
Уловили?
Для того чтобы правильно посчитать дельту времени (время полёта i-того снаряда) нам ДОСТАТОЧНО знать:
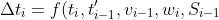)
По порядку.
абсолютное время старта снаряда.
абсолютное время попадание в зонд предыдущего снаряда.
скорость зонда после попадания в него предыдущего снаряда
скорость данного снаряда.
общая дистанция, которую зонд уже прошел до последнего столкновения (ускорения).
У нас в модели (в предыдущих строчках) все это есть.
Я нарисовал случай

То есть снаряд выстрелили до того как произошло столкновение зонда с последним снарядом. При этом заметно меньше. Не произошло даже предпоследнее столкновение. Но видно что все эти столкновения уже не важны. Все можно получить из последнего (результат предыдущих уже интегрирован в S
i-1)
Из рисунка.

путь зонда до столкновение с нашим i-тым снарядом

путь снаряда
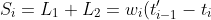+ w_iT_2)
оба пути равны. Отсюда выражаем интервал T
2}{w_i-v_{i-1}})
и окончательно искомая дельта
}{w_i-v_{i-1}}+(t'_{i-1}-t_i))
И вот смотрите. Если

?
Наша формула вырождается в первоначальную, "неправильную". То есть. Если снаряд стартует ровно в тот момент, когда предыдущий попал в зонд, то эта формула работает. Но это - частный случай.
Хорошо. А что если...

?
Ответ - ничего. Та же самая формула что мы вывели выше. Просто T
1 становится отрицательным и вычитается из T
2Графическая интерпретация такого решения.

Я еще не испытывал это решение. Но по-моему все правильно. Или я ошибаюсь?
Все это сработает, если снаряды не перемешаются.
Конечно, пока что они и не будут. Так как все летят с одной скоростью. Но мы рвемся к более сложной модели. Отладим простую - перейдем к сложной.
Но выловить перемешивание (и неадекватность модели) просто. Для этого и фиксируется абсолютное время столкновения. Если i-тое меньше i-1, это легко выловить автоматически в том же Excel-е, скажем условным форматированием (подсветить это место красным).
Почему таблицы?
Да потому что это проще всего и как по мне (прикладному программисту со стажем) наглядней. Я таблицы для себя открыл уже изучив кучу языков и натаскавшись в базах данных и влюбился в них с первого взгляда. Тут операнды не отделены от операторов и можно ВОЯТЬ на ходу решения, не зная наперед какое оно в итоге будет (в программировании сначала надо все понять в уме, а потом уже писать код, операторы, после чего применять это к операндам, отдельно заготовленным данным). В общем, как художнику мне тут легче.

Если кто не понял до сих пот что такое эта моя "модель для сборки". Это вот это:

То есть таблица цифр. Строчки это математическая модель полёта i-того снаряда. Данные рассчитываются слева на права ну и что-то берётся из строчки выше (i-1). Вот это как правило путешествует справа налево (вниз). Динамика событий - колонка. Из них можно получать график, показывающий динамику. В нулевой строчке ставятся некие начальные значения (в строчке 1 где в формуле участвует ссылка i-1). Конечно в таком виде мало что можно из модели понять. Поэтому надо еще уметь из этой таблицы вынимать всякие общие цифры (бардак вверху видите? это я нахватался сразу что мне было интересно) и графики. На самом деле тут еще работать и работать. Поэтому саму excel-ку не выкладываю. Нечего пока выкладывать.
Главное. Если на простом луче (когда масса снарядов и скорость у всех равны) модель заработает, "полетит" можно будет попробовать варьировать скорость и массу снарядов на старте и смотреть что же в итоге получится. Должно быть очень интересно!
