Дуга это еще не время путешествия разных светил, тем более, с разной скоростью.
Лады.
Разберем численно эту задачу, приняв ряд упрощений. Не будем учитывать наклон земного экватора к плоскости эклиптики, а также 5-градусный наклон плоскости лунной орбиты к экватору Земли. Также не будем брать во внимание слегка неравномерное движение Солнца и Луны на небе, обусловленные эксцентричностью орбит Земли и нашего спутника. Наблюдателя же посадим где-нибудь на экваторе, чтобы каждые сутки и Солнце, и Луна «пробегали» прямо у него над головой, т.е. проходили через зенит. Такие кульминации светил будут происходить с периодами P1 и P2.
Для Солнца этот период будет равен P1= 24 часа = 86 400 секунд.
Для периода Луны возьмем среднюю продолжительность лунных суток P2= 24 часа 48 минут = 89 280 секунд.
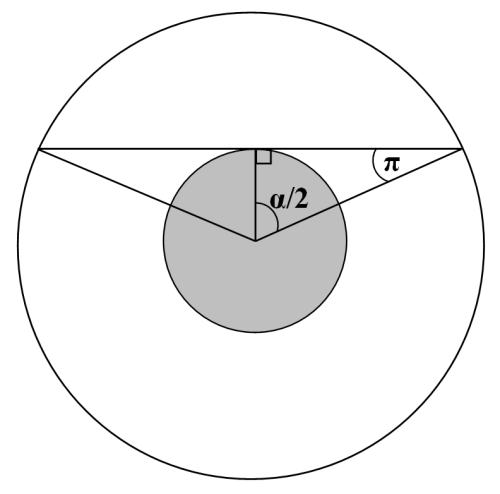
Из рисунка видно, что угол α/2, стягивающий половину видимого пути светила над горизонтом, равен:
α/2 = 90° – π
где π – горизонтальный параллакс светила. Значения горизонтальных параллаксов Солнца и Луны, соответственно, составляют 9" и 57'.
Тогда полный угол, стягивающий всю дугу видимого пути над горизонтом Солнца или Луны, составит:
α = 180° – 2π
Для Солнца этот угол составит α1 = 179° 59' 42", для Луны α2 = 178° 06' 00"
За полный видимый оборот период нахождения светила над горизонтом составит:
t = P • α / 360°
(рефракцию во внимание не беру)
Таким образом, за одни средние солнечные сутки Солнце будет находиться над горизонтом:
t1 = 43 198,8 секунд
В свою очередь, Луна за одни средние лунные сутки будет пребывать над горизонтом:
t2 = 44 168,8 секунд
Теперь выберем период, за который будем считать суммарную продолжительность нахождения Солнца и Луны над горизонтом наблюдателя. Я взял вполне скромный промежуток в 90 дней. Чем он удобен? В нем ровно 90 средних солнечных суток и почти ровно 87 средних лунных суток.
В результате имеем суммарное время нахождения Солнца над горизонтом наблюдателя за 90 суточный интервал времени:
T1 = 90 • t1 = 3 887 892 секунд
Для Луны это суммарное время, соответственно, будет равно:
T2 = 87 • t2 = 3 842 686 секунд
Считаем искомую разницу за 90-дневный интервал времени:
∆T = T1 – T2 = 45 206 секунд ≈ 12,5 часов.
По-моему, не хило «набежало»
