Честно говоря, я вообще не понимаю о чем тут речь?
Я так понял это была шутка.
Но она затянулась?
Сила светового давления на идеальное зеркало при строго отвесном падении:
F/S=P=Ws/c.
Где Ws – плотность потока световой энергии (Ватт/м2), с – скорость света.
Световой поток от Солнца у Земли ~ 1400 Ватт/м2
Считаем давление: 4,67E-06 Н/м2
Уже на орбите Земли давление света – мизерное. Если у вас поверхностная плотность паруса 0.1 г/м2 (это почти ничто 10^-4 кг/м2), то ускорение которое вы получаете у Земли при таком парусе a=4,67E-06/0,0001 =0,0467 м/с2.
Меньше 5 тысячных g!
Для того чтобы получить заметное ускорение вам нужно...
Во-первых еще лучшая поверхностная плотность паруса чем "ничто". "Нанопарус" в 10^-6 кг/м2 –уже годится для межзвездного полета (он практически прозрачен).
Но и этого будет мало.
Во-вторых вам надо для начала разгона приблизится к Солнцу как можно ближе.
Потому что тут работает закон обратных квадратов.
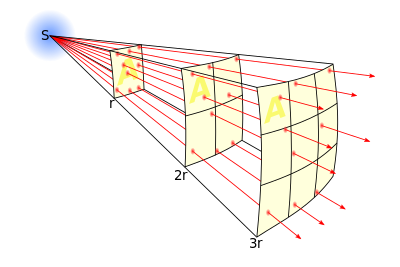
Если вы приблизились к точечному источнику света в N раз, поток увеличился в N^2 раз.
Удаляетесь в N раз, поток энергии падает в N^2 раз.
А значит и давление а значит и ускорение.
Пройдя у Солнца на расстоянии 0.1 а.е. (это 1/10 расстояния от Земли до Солнца) мощность (а значит и давление) возрастает в 100 раз.
Считаем ускорение для легкого паруса (10^-6 кг/м2).
У самого Солнца 0,1 а.е. – 467 м/с2. Парус "срывается с места" и начинает удаляться. Но пересекая орбиту Меркуния 0.4 а.е. его ускорение уже упало до 29,2 м/с2. Он продолжает удалятся. Пересекая орбиту Земли его ускорение "всего" 4,67 м/с2 (пол g!!!)
Но закон обратных квадратов все больше и больше съедает давления света по мере удаления паруса.
Пересекая орбиту Юпитера 5 а.е. ускорение уже 0.2 м/с2
А пересекая орбиту Плутона 40 а.е. 0,003 м/с2
Там фактически, скорость парусника уже почти не прирастает. Почти вся скорость что он набрал – он набрал еще до орбиты Земли. Пересекая орбиту Плутона он уже считай в инерциальном полете. Не то что свет другой звезды – своей уже практически не действует.
Теперь он летит по инерции до тех пор пока по закон обратных квадратов для света звезды-цели не начнет заметно его скорость. И это опять же начнет проявляться ну 20 а.е. до звезды или те же 40 а.е. А скорей всего все 10 а.е. (все зависит еще и от звезды. С красными карликами у нас будет просто беда)
При этом надо же понимать (если это не шутка) первый закон Ньютона!
Тело находится в состоянии покоя или равномерного прямолинейного движения если на него не действует никакая сила или действия всех сил компенсируется. Набранная у поверхности Солнца скорость парусника после удаления его от светила никуда не девается. Она "накапливается".
Какова максимальная скорость, которую может парусник получить при таком выстреле "от солнца"?
Вот ссылка:
http://path-2.narod.ru/02/02/sss.docТут все расчетные форумы есть. В самом начале.
И есть таблица результатов.
Хотя при нынешних вычислительных возможностях легко построить в Excel и разностную модель которая бы была бы не менее точна и учитывала еще и разные осложняющие аналитический вывод нюансы (например постепенное открытие паруса, сброс балласта и т.д.). Единственный нюанс. В начале надо брать квадратично меньший шаг расчетной модели dx. По мере удаления – можно удленить и шаг.
