Формул много, а главной --- связывающей размеры пылинок, паруса и их скорость с размером пробоя ---- нет....
"Главаная х-формула" есть.
Хотя AlexAV нас от нее берег, не желая, видимо, травмировать юношеские души этим безобразием, но юноши же хотят! Я сам захотел таки, поняв что без нее - никак! В четверг-пятницу уже захотел!
И я думаю, вот она (если не она - Alex поправит):
^2 \ln \left[ \frac{2m_e c^2 \beta^2}{I(1-\beta^2)}-\beta^2 \right])
Вот она красавица! Обратите внимали! Дифура и очень гадостная дифура (надо сказат!)
Здесь:
 ; \beta=\sqrt{1-\left( \frac{E}{mc^2}+1 \right)^{-2}})
И это еще не все прибамбахи в ней.
Называется: формула Бете-Блоха.
Потеря энергии любой заряженной частицы любой энергии в любом материале.
Есть масса ее версий в сети (все изгаляются и дополняют как могут), но это взята с английского сайта "вики".
Bethe_formulaНе пользуйтесь никакими другими (ни русской ни украинской) ибо там надо четко понять в каких размерностях что приведено. Я замучался с ними. А эту я "плюс-минус лапоть" проверил (по известному пробегу альфа-частицы в алюминии). То есть размерности все сходятся. А расхождения из-за очень грубой аппроксимации что я сделал.
Правда, я сразу использовал упрощенную версию для бэтте << 1:
\Delta h)
Здесь уже не нужны релятивистские энергии и скорости:

На 0,1с и даже на 0,25с вполне можно пользоваться физикой Ньютона.
Только уже на 0,5с надо начинать использовать релятивистский вариант (да и то погоды это там не сделает).
Самое главное. Во-первых я заменил дифференциал на дельту (ибо у нас будет очень короткий участок торможения и диффуру нам тут решать вообще не надо). Во-вторых я заменил x на h ибо дистанция потери энергии - как раз толщина паруса h
Обратите внимание на квадратные скобки. По сути нужный нам для работы вид у формулы вот такой:
\ h)
Не такой страшный. Ее непременно надо решать по частям. Я специально разбил формулу на подформулы чтобы было меньше считать (скажем если вам все же захочится считать пробег численным интегрированием, то лучше ее оптимизировать так вот).
Первая скобка А
2 - это заряд электрона в квадрате на 4-е пи на электрическую постоянную. Вообще один раз посчитать для всех случаев жизни: А
2 = 5,32252E-56 чего-то там (можете пересчитать и перепроверить) и подставлять везде.
Вторая B и третья C скобки считаются для конкретного материала препятствия и конкретного типа частицы (тоже один раз):
m
e - масса электрона (обратите внимание, масса самой частицы тут никаким боком!)
Z - заряд частицы (буквально - номер в таблице Менделеева)
n - концентрация электронов в среде торможения. Считается так:

N
A - число Авогадро.
Z' - заряд вещества препятствия
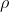
- плотность вещества препятствия
Mu - молярная масса (на украинском сайте написана лажа!)
Тут главное не напутать с размерностями. Если у вас молярная масса в г/моль, то плотность тоже брать в грамм на … лучше м3. Я лично от греха подальше все считаю в СИ.
В третьей скобке остался один неясный параметр I - средний ионизационный потенциал:

Обратите внимание, я его тут сразу перевожу из эВ в Дж. Если вы все считаете в эВ, то умножать на 1.6E-19, разумеется, не надо.
В общем, для нашей задачи, ПРИТОРМАЖИВАНИЯ теперь у нас все есть (а вот если считать пробег с окончательным торможение, то, например, я тут задолбался выкручивать дифуры и кажется ничего путевого получить тут нельзя, ну и ладно - об этом отдельно).
В общем. Зная толщину паруса h, зная материал паруса, плотность, Z' и зная материал пылинки, ее Z, мы легко считаем долю потерянной энергии дельта-E/E (на начальную энергия) при прохождении той на скорости v нашего паруса.
Кто тут страдал, что не знает как посчитать все это? Пробуйте!
Вадим, как вы считаете эту долю! Поделитесь!
Без всякого, умудрения в сложности....по пионерски...
Зная из учебника что 14,1 мэв нейтрон движеться со скоростью 56 000 км/с, экстраполируем его энергию на 0.1с, получаем 3,9 мэв, на нуклон. Атом углерода состоит из 12 нуклонов, значит получается 47мэв. Алекс нам дал табличные данные, торможения иона углерода в алюминии 550эв/нм. Для 40 нм паруса это, 22кэв(и откуда мне 27 приснилось) Делим одно на другое. Получаем 0,046%...чуть более правильная цифра.
Я для углерода (массовое число 12) в алюминии по всей выше описанной кабалистике на скорости 0.1с получил k=
0,003459243 %! 3,12E-16/9,02E-12=3,46E-05.Окончательная поправка 2,81E-15/9,02E-12 =3,11E-04. То есть 0,0311%!Это все, разумеется, черновики (сами знаете как я считаю, раз раз и что-то потерял!). Надо сесть и все хорошенько переделать, красиво оформивши, если это все - движение в верном направлении.
Теперь. Еще горстка простеньких уравнений.
^2; k\rightarrow 0 ; Q \rightarrow \Delta E)
Это уже выжимка из моего спора с Alex_AV в котором он по сути оказался прав.
Если у нас полу-упругое соудорение, то можно считать что вся потерянная частицей энергия превратилась именно в тепло. Я взял m=m_b и получил вот такую красивую кривулю:

И так. Если пылинка только слегка притормаживает, то она теряет очень небольшую часть энергии (которую мы считаем из Бете-Блоха) и смело считаем что вся эта энергия превращается в паразитное тепло.
По-сути действительно, не было смысла считать сохранение импульса. Я зря поднял кипишь. Ну разве что у меня получилось много интересных приключений ума. Я вдруг обнаружил, что не учитываю половины возможных столкновений. Ну да ладно. Это уже не к делу.
И так. Выделенная пылинкой энергия Q найдена. Что дальше?
Дальше я предлагаю ее смело поделить на 2 (таки поделить все-таки!).
Почему?
Потому что все относительно. Если вы гном, сидящий на пылинке то вы видите как на вас налетает участок паруса и он слегка притормаживая, теряет Q своей энергии. Но если вы другой гном, которые сидит на парусе, то вы видите как на парус налетает пылинка и слегка притормаживая, теряет в парусе Q своей энергии. Так кто и где теряет? Пылинка в парусе или парус в пылинке? Если условно считать что масса пылинки примерно равна массе участка паруса через который она прошла то всем участникам столкновения досталось поровну по Q/2.
Логично?
Если пылинка больше - больше досталось ей. Если пылинка меньше - больше досталось парусу. Но у нас типичная пылинка сравнима с толщиной паруса. Значит зная размер и плотность пылинки считаем паразитное Q_p:

А из него, зная L - теплоту испарения паруса, считаем радиус дырки которая испарится этой паразитной энергией, если вся она пойдет на испарение паруса.

Так и получается в расчетах дырка в несколько микрон.
На самом деле это очень хилая цифра. Реальный диаметр может быть больше. Если вместо теплоты испарения L взять теплоту плавления. Но (что вселяет надежду) реальный размер может оказаться и меньше. Ведь в последнем расчете не учитывается рассеивание энергии за то время, за которое выделившаяся после прохождения пылинки энергия будет испарять парус. Мы эти утечки тут НИКАК не посчитали. А они наверняка будут. И как мне кажется, очень даже нехилыми.
Поэтому я перерисовал старый рисунок. Хотя радиус дырки R нам все еще не ясен, но качественно картина выглядит следующим образом:

Пылинка проходит парус (стадии 1,2) практически не останавливаясь в нем и не забирая из него материю (масса и скорость ее остается практически той же). Небольшая часть материи паруса приобретает небольшую скорость (компенсация потери импульса) но это, как насчитал Alex_AV, крохи, пара км/с, и по-сути в динамике процесса никак не играет, хотя я все же показал маленькую синюю стрелочку обозначающую этот нюанс.
Самое главное. Пройдя через парус за мгновение, время t ~ 10^-15с, пылинка оставила в ней половину выделившегося тепла. Q_p =Q/2 и это тепло теперь, как уверяет Alex, на скорости Ферми (~1 Мм/с) начинает расползаться по парусу.
Тут уже начинаются куда более медленные процесс. Это уже наверное наносекунды.
Пылинка со своей половиной тепла уже улетела испаряться и рассеиваться далеко назад (я показал ее слишком близко потому что ограничен жанром иллюстратора), а вот то что происходит с парусом теперь - вопрос открытый.
Для знатоков в области физики плазмы.
Как живописец, я показал, что с торцов растекающегося цилиндра поражения во все стороны улетают сверхгорячие электроны. Я показал, что из тела паруса навстречу разбегающимся горячим электронам несутся относительно холодные (хотя они тоже греют парус омически, что я тоже живописал цветом). Но эта сложная качественная картина нуждается в еще более сложном количественном расчета.
В итоге мы имеем то, что имеем.
Диаметр дырки все еще открыт (хотя зона незнания заметно сузилась).
Формула то есть. Процесс понимания сути проблемы, я думаю, медленно но идет.
А вот счастья нет!
Как говорил Дуримартус, пытаясь осушить болото зловредной Тротилы, еще 423 578 ведер, и золотой ключик у нас в кармане!

Вопросы, замечания?